матриці

1. Множення на матрицю
2. типи матриць
3. Матриці зсуву (Translate Matrix)
4. Матриці масштабування (Scale Matrix)
5. Матриці обертання (Rotate Matrix)
6. комбіновані матриці
7. Множення матриці не коммутативно
8. Одинична матриця (матриця ідентичності, Identity Matrix)
9. Приклади застосування матриць

Матриці і обумовлені ними трансформації є однією з основ тривимірної графіки. У попередній статті Вектора, матриці, трансформації я вже розповідав про матрицях, але дуже поверхово. Тепер мені б хотілося детально пояснити вам що таке матриці, з яких елементів вони складаються, що ці елементи означають, навести приклади використання матриць, розповісти про примноження матриць, які матриці найчастіше використовуються в графіку і іграх і як вони виглядають, а так само багато інше. Мені б хотілося, що б Ви детально розбиралися в операціях над матрицями і могли, в разі необхідності, самостійно "зібрати" потрібну вам матрицю, не вдаючись до вбудованим функціям DirectX, тому як іноді це буває потрібно.

Множення на матрицю

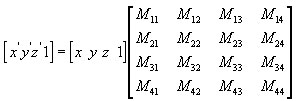Як правило, матриця служить для перетворення вектора. Як я вже говорив в попередньому уроці, кожна матриця визначає перетворення координат з однієї системи координат в іншу. Тобто множення вектора на матрицю якимось чином трансформує вектор, переводячи його координати в іншу систему координат. Щоб це Вас не бентежило, ще раз наведу максимально простий приклад: вважаємо центром однієї системи координат двері, а інший системи координат - вікно, в цьому випадку помноживши координати будь-якого предмета, пораховані щодо двері на матрицю перетворення з системи координат двері в координати вікна, ми отримаємо координати предмети щодо вікна (тобто в системі координат вікна). Загалом, все просто. Справа Ви бачите повну формулу множення вектора на матрицю - саме по ній вважаються всі перетворення, математика рівня 6го класу середньої школи)))

типи матриць

Не слід розуміти заголовок цієї частини тексту так, ніби є абсолютно різні і особливі типи матриць, які чимось абсолютно унікальні. Я називаю їх типами просто для зручності - насправді матриця, вона і є матриця і відрізняються матриці лише значеннями їх окремих елементів, не більше того. При цьому так само треба щоб Ви розуміли, що я намагаюся пояснювати "на пальцях", так, що б зрозуміла кожна - з математичної точки зору все, м'яко кажучи, дещо складніше. Я ж лише просто розповім і покажу те, що Вам потрібно знати для того, що б Ви могли не відчувати особливих труднощів з матричної арифметикою і могли розуміти як працюють перетворення вертексов / моделей / нормалей і т.д. в ваших програмах.

Отже, матриці можна розділити на чотири умовні типи:

1. матриці зсуву
2. матриці обертання
3. матриці масштабування
4. Інші матриці (наприклад, перспективні або комбіновані з перших трьох типів)

Матриці зсуву (Translate Matrix)

Матриці зсуву це найпростіше, що тільки можна собі уявити. Вони задають просто "зрушення" по кожній з осей координат на певне значення. Цей зсув зберігається в нижньому рядку матриці (в перших трьох її значеннях, які вище позначені як М41, М42, М43). Якщо ми поставимо в них, наприклад (0, 10, 99), то в результаті трансформації будь-якого вектора цією матрицею, він зрушить на 0 по осі X, на 10 по осі Y і на 99 по осі Z. Мені здається, зовсім не складно , правда ж?

Матриці масштабування (Scale Matrix)

Що роблять матриці цього типу, теж зовсім нескладно здогадатися - вони масштабують. Коефіцієнти масштабування вздовж кожної осі задаються діагональними елементами матриць: М11 для осі X, М22 для осі Y і М33 для осі Z.

Матриці обертання (Rotate Matrix)

Цей тип матриць дещо складніше, ніж попередні. Тому і зрозуміти його треба трохи краще, розібратися що до чого і з чого воно йде. Для обертання 2х-мірного вектора, як відомо, використовується така формула:

a = угол_поворота; new_x = old_x * cos (a) - old_y * sin (a) new_y = old_x * sin (a) + old_y * cos (a)

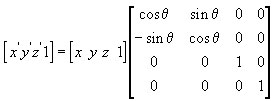А ось так вона виглядає у вигляді матриці, подивіться, відмінностей зовсім не багато ... точніше їх взагалі немає. Оскільки "обертаються" координати X і Y - саме обертання задається тільки в перших 2 * 2 осередках. Простіше кажучи - обертання вказується саме для тих осей, навколо яких відбувається обертання. А решта, третя, вісь (третій стовпець + третій рядок), залишається незмінною - там тільки діагональна одиниця стоїть.

Ось, подивіться на матрицю обертання навколо осі X - 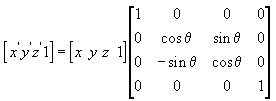Тут "не використовуються" (тобто стоять початкові нулі і діагональна одиниця) перший рядок і перший стовпець. Сподіваюся, я зрозуміло пояснюю? Просто подивіться уважніше на картинку і спробуйте споставіть з тим, що я говорю. Якщо Ви це зрозумієте - у Вас вже ніколи більше не виникне плутанини з матрицями і все завжди зможете хоч серед ночі з закритими очима правильно написати все три матриці обертання.

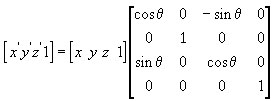Аналогічно відбувається і з матрицею обертання щодо осі Y. Ви ж розумієте про що я?

Думаю, розумієте. Це ж просто. Або це мені так тільки здається? Якщо Вам не зрозуміло - терміново пишіть в коментарі і будемо розжовувати далі, поки не настане момент повного просвітлення. Без знання цієї теми далі Вам в комп'ютерній графіці робити просто напросто нічого ...

комбіновані матриці

Скомбінувати дві або більше матриць в одну абсолютно не проблематично, для цього досить просто помножити ці матриці. Наприклад, якщо помножити матрицю обертання, масштабування і зсуву, то множимо об'єкт відповідно, повернеться, відмасштабуйте, і зрушиться.

Слід розуміти, що все трансформації, які робить матриця над вектором, вона робить відносно початку системи координат. Ніяких інших варіантів просто НІ - запам'ятайте це !!!! Не можна, наприклад, повернути вектор щодо якоїсь точки звичайної матрицею повороту. Але що ж робити, якщо саме таке завдання і стоїть? Все дуже просто - треба зробити три матриці:

1. Матриця зсуву. Така, що б точка, навколо якої буде повертати (або обертати) збіглася з початком системи координат. Наприклад, якщо треба зробити трансформацію щодо точки (10, 20, 30), треба зробити матрицю зсуву на (-10, -20, -30)
2. Матриця потрібної нам трансформації. В даному випадку ми вели мову по поворот, тому матриця повороту
3. Матриця "зсуву на місце", тобто зворотна першої матриці, зрушення не на (-10, -20, -30), а на (10, 20, 30)

Після цього помножити їх один на одного і отримати кінцеву матрицю. І ось вона вже буде робити те, що нам і потрібно, а саме, обертання навколо зазначеної нами точки:

матріца_результірующая = зрушення * обертання * обратний_сдвіг;

Множити матриці вмієте? Якщо немає, ось просте правило: щоб помножити дві матриці, потрібно кожен рядок першої матриці помножити на кожний стовпець другуматриці. Помноживши перший рядок першої матриці на кожен стовпець другуматриці ми отримаємо всі елементи першого рядка матриці твори, потім робимо те ж саме для другого рядка першої матриці і т.д. Малюнок в даному випадку пояснить краще, ніж я:

Я сподіваюся, що зрозуміло - не можу придумати, як пояснити краще.

Множення матриці не коммутативно

Запам'ятайте це раз і назавжди! Тобто Мата * матБ зовсім не має дорівнювати матБ * Мата! Це найважливіше правило, не забувайте про нього ніколи. Пояснюю в картинках: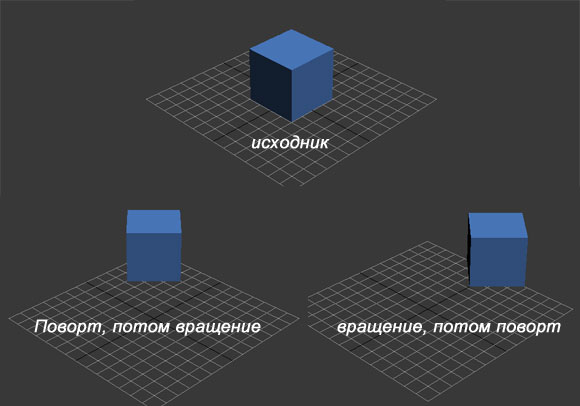

Бачите різницю в положенні кубів на сітці? Від порядку застосування матриць залежить кінцевий результат - про це треба завжди пам'ятати.

Одинична матриця (матриця ідентичності, Identity Matrix)

Одинична матриця це та матриця, яка не виробляє ніяких трансформацій. У ній все нулі, а по діагоналі одиниці.

Приклади застосування матриць

Крім того, що ми можемо просто задавати матрицями положення об'єкта в просторі, матриці можуть допомогти нам і легко зв'язати положення предметів один до одного. Припустимо, що у нас є якась "база для вентилятора" і є сам вентилятор (лопаті). Ми можемо поставити становище і того і іншого в світі гри у вигляді матриць. Але ми можемо зробити краще! Ми можемо прив'язати вентилятор до його "базі". При цьому, під час відтворення, положення самого вентилятора (лопатей) буде здаватися не тільки його матрицею, але і матрицею того, до чого він пріявзан, тобто буде вважатися так:

матріца_результ = матріца_лопасті * матріца_база

Як підсумок - якщо ми почнемо трансформувати (рухати, обертати) базу вентилятора - слідом за нею будуть рухатися і лопаті! Самі! Без будь-якого нашого участі!

Вентилятори в грі Alien Moon прив'язані до баз, що сильно спрощує роботу з ними

Теж не дуже короткий і не особливо простий урок вийшов, однак) Чекаю ваших коментарів !!!

Ще по цій темі: