Наукова Мережа >> Курс лекцій І.М.Гельфанда з лінійної алгебри
- 1 Визначення сполученого простору.
- 2 біортогональних (взаємні) базиси.
- 3 Взаємозамінність і.
- 4 Перетворення координат в і.
- 5 Простір, поєднане до евклидову.





Next: 24 тензори Previous: 4 Поняття про тензори
1 Визначення сполученого простору.
нехай  - лінійний простір. Одночасно з
- лінійний простір. Одночасно з  часто розглядають інше, тісно пов'язане з ним простір, так зване поєднане простір. Для того щоб сформулювати визначення сполученого простору, повернемося до поняття лінійної функції, введеному нами в п. 1 §4.
часто розглядають інше, тісно пов'язане з ним простір, так зване поєднане простір. Для того щоб сформулювати визначення сполученого простору, повернемося до поняття лінійної функції, введеному нами в п. 1 §4.
Лінійною функцією ми назвали функцію 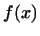 ,
, 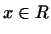 задовольняє умовам:
задовольняє умовам:
1 
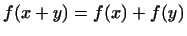 ,
,
2 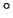
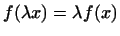 .
.
нехай  - базис в
- базис в 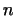 вимірному просторі
вимірному просторі  . якщо
. якщо
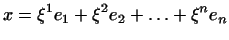
- вектор з  , То лінійна функція в
, То лінійна функція в  може бути записана у вигляді (див. §4)
може бути записана у вигляді (див. §4)
де коефіцієнти 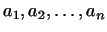 , Що визначають лінійну функцію, обчислюються за формулами
, Що визначають лінійну функцію, обчислюються за формулами
Як це ясно з формули ( 1 ), При заданому базисі  всяким
всяким 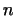 числах
числах 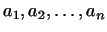 відповідає лінійна функція, до того ж лише одна.
відповідає лінійна функція, до того ж лише одна.
нехай 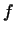 і
і 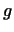 - лінійні функції. Їх сумою називається функція
- лінійні функції. Їх сумою називається функція 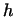 , Що ставить у відповідність кожному вектору
, Що ставить у відповідність кожному вектору 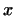 число
число 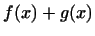 . Твором лінійної функції
. Твором лінійної функції 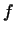 на число
на число 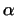 називається функція, яка має у відповідність кожному вектору
називається функція, яка має у відповідність кожному вектору 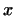 число
число 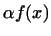 .
.
Очевидно, що сума лінійних функцій і твір лінійної функції на число є знову лінійна функція. При цьому, якщо лінійна функція 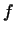 задається числами
задається числами 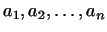 , а
, а 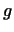 - числами
- числами 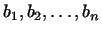 , то
, то 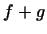 задається числами
задається числами 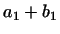 ,
, 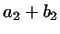 ,
,  ,
, 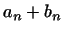 , а
, а 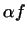 - числами
- числами 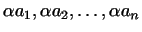 .
.
Таким чином, безліч заданих в  лінійних функцій утворює лінійний простір.
лінійних функцій утворює лінійний простір.
Визначення 23.1 Нехай  є
є 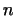 -мірним простір. простором
-мірним простір. простором  , зв'язаних до
, зв'язаних до  , Ми назвемо лінійний простір, векторами якого є лінійні функції, задані в
, Ми назвемо лінійний простір, векторами якого є лінійні функції, задані в  . сума в
. сума в  визначається як сума лінійних функцій, а твір вектора з
визначається як сума лінійних функцій, а твір вектора з  на число - як твір лінійної функції на число.
на число - як твір лінійної функції на число.
Так як при заданому базисі  в просторі
в просторі  кожна лінійна функція однозначно задається системою
кожна лінійна функція однозначно задається системою 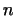 чисел
чисел 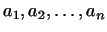 , Причому сумі функцій відповідає сума чисел, твору функції на
, Причому сумі функцій відповідає сума чисел, твору функції на 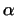 твір чисел
твір чисел 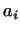 на
на 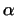 , То ясно, що
, То ясно, що  ізоморфно простору, в якому вектор визначений як сукупність
ізоморфно простору, в якому вектор визначений як сукупність 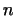 чисел.
чисел.
Значить, простір  , Поєднане до
, Поєднане до 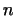 -мірним простору
-мірним простору  , також
, також 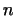 -мірним.
-мірним.
якщо простору  і
і  розглядають одночасно, то вектори з
розглядають одночасно, то вектори з  називаються контраваріантнимі , А вектори з
називаються контраваріантнимі , А вектори з  коваріантними . Надалі символи
коваріантними . Надалі символи 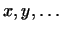 означатимуть елементи з
означатимуть елементи з  , Тобто контраваріантниє вектори, а
, Тобто контраваріантниє вектори, а 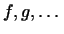 - елементи з
- елементи з  , Тобто коваріантні вектори.
, Тобто коваріантні вектори.
2 біортогональних (взаємні) базиси.
Надалі ми будемо значення лінійної функції 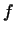 в точці
в точці 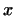 позначити через
позначити через 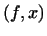 . Таким чином, кожній парі
. Таким чином, кожній парі 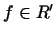 і
і 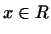 віднесено число
віднесено число 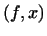 , причому
, причому
1 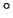
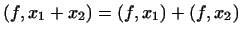 ,
,
2 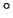
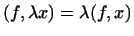 ,
,
3 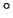
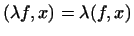 ,
,
4 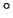
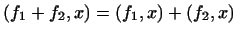 .
.
Перше і друге з цих співвідношень - це записані в нових позначеннях рівності
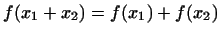
і 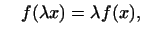 є визначенням лінійної функції, а третє і четверте - визначення твори лінійної функції на число і суми лінійних функцій. співвідношення 1
є визначенням лінійної функції, а третє і четверте - визначення твори лінійної функції на число і суми лінійних функцій. співвідношення 1  -4
-4  нагадують за зовнішнім виглядом аксіоми 2
нагадують за зовнішнім виглядом аксіоми 2 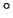 і 3
і 3 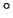 скалярного твори (§2). Треба лише підкреслити, що в той час, як скалярний твір є число, віднесене парі векторів одного і того ж (евклидова) простору,
скалярного твори (§2). Треба лише підкреслити, що в той час, як скалярний твір є число, віднесене парі векторів одного і того ж (евклидова) простору, 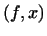 є число, віднесене парі векторів, один з яких належить аффинного простору
є число, віднесене парі векторів, один з яких належить аффинного простору  , А інший - аффинного простору
, А інший - аффинного простору  .
.
вектори 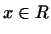 і
і 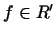 ми назвемо ортогональними, якщо
ми назвемо ортогональними, якщо
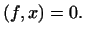
Таким чином, хоча в афінному просторі  (На відміну від евклидова) немає поняття ортогональності двох векторів
(На відміну від евклидова) немає поняття ортогональності двох векторів 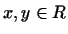 , Можна говорити про ортогональності векторів з
, Можна говорити про ортогональності векторів з  до векторів з
до векторів з  .
.
Визначення 23.2 Нехай  - базис в
- базис в  , а
, а 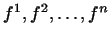 - базис в
- базис в  . Ми назвемо ці базиси біортогональних (взаємними) , якщо
. Ми назвемо ці базиси біортогональних (взаємними) , якщо
введемо символ 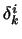 , поклавши
, поклавши
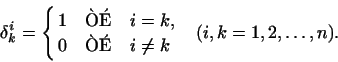
тоді 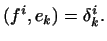
якщо  - базис в
- базис в  , то
, то 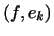 є числами
є числами 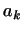 , Що визначають лінійну функцію
, Що визначають лінійну функцію 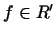 [См. формулу ( 2 )], так як
[См. формулу ( 2 )], так як 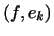 є інша форма запису виразу
є інша форма запису виразу 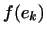 .
.
З цього зауваження випливає твердження:
якщо  - довільний базис в
- довільний базис в  , То в
, То в  існує, і до того ж тільки один, базис
існує, і до того ж тільки один, базис 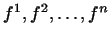 такий, що базиси
такий, що базиси  і
і 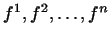 біортогональних (взаємні).
біортогональних (взаємні).
Дійсно, з рівності ( 3 ) маємо
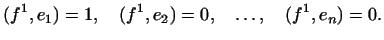
Таким чином, тут задані числа 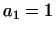 ,
, 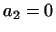 ,
, 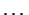 ,
, 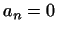 . Так як по всяких числах
. Так як по всяких числах 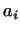 можна побудувати єдину лінійну функцію, то
можна побудувати єдину лінійну функцію, то 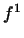 визначено, і при цьому однозначно. аналогічно визначається
визначено, і при цьому однозначно. аналогічно визначається 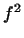 равенствами
равенствами 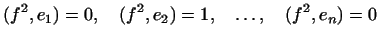 і т.д. побудовані вектори
і т.д. побудовані вектори 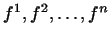 з
з  (Лінійні функції) лінійно незалежні, так як відповідають кожному з них системи чисел
(Лінійні функції) лінійно незалежні, так як відповідають кожному з них системи чисел 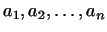 лінійно незалежні між собою. Ми побудували, таким чином, базис, біортогональний базису
лінійно незалежні між собою. Ми побудували, таким чином, базис, біортогональний базису  і довели його єдиність.
і довели його єдиність.
Надалі ми будемо користуватися прийнятими в тензорному обчисленні позначеннями, а саме, якщо в деякому виразі один і той же індекс варто один раз вгорі, а інший раз внизу, то це означає, що за цим індексом проводиться підсумовування (від 1 до 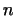 ). Сам знак підсумовування
). Сам знак підсумовування 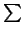 ми при цьому будемо опускати.
ми при цьому будемо опускати.
наприклад, 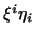 означає
означає 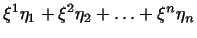 .
.
маючи в  і
і  біортогональні базиси, легко обчислювати координати будь-якого вектора. нехай
біортогональні базиси, легко обчислювати координати будь-якого вектора. нехай 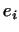 і
і 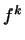 - біортогональні базиси. знайдемо координати
- біортогональні базиси. знайдемо координати 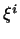 вектора
вектора 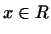 в базисі
в базисі 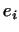 . Ми маємо
. Ми маємо
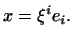
Звідси 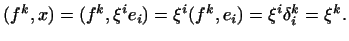
Отже, координати 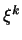 вектора
вектора 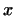 в базисі
в базисі  обчислюються за формулами
обчислюються за формулами

де 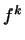 - базис, взаємний з базисом
- базис, взаємний з базисом 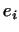 .
.
Аналогічно отримуємо, що координати 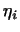 вектора
вектора 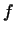 в базисі
в базисі 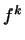 обчислюються за формулами
обчислюються за формулами
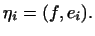
нехай  і
і 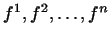 - два взаємних (біортогональних) базису. висловимо величину
- два взаємних (біортогональних) базису. висловимо величину 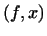 через координати векторів
через координати векторів 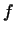 і
і 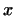 в базисах
в базисах  і
і 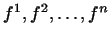 відповідно. нехай
відповідно. нехай
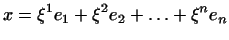
і 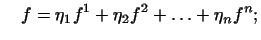 тоді
тоді 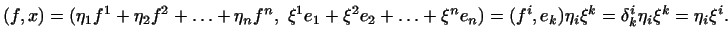
Отже, якщо  - базис в
- базис в  ,
, 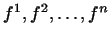 - взаємний з ним базис в
- взаємний з ним базис в  , то
, то
де 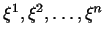 - координати вектора
- координати вектора 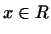 в базисі
в базисі  , а
, а 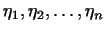 - координати вектора
- координати вектора 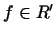 в базисі
в базисі 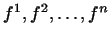 .
.
зауваження Якщо  і
і 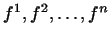 - довільні базиси в
- довільні базиси в  і
і  відповідно, то
відповідно, то
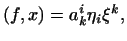
де 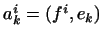 .
.
Ми бачимо, що у взаємних базисах значення 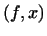 записується особливо просто.
записується особливо просто.
Отже, ми побудували відповідність, відносить кожному лінійному простору  інший простір, а саме поєднане простір
інший простір, а саме поєднане простір  . Ми можемо тепер встановити відповідність між лінійними перетвореннями просторів.
. Ми можемо тепер встановити відповідність між лінійними перетвореннями просторів.
нехай 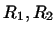 - два лінійних простору і
- два лінійних простору і 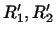 - простору, їм пов'язані. Кожному лінійному перетворенню
- простору, їм пов'язані. Кожному лінійному перетворенню 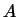 простору
простору 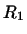 в
в 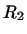 ми поставимо у відповідність лінійне перетворення
ми поставимо у відповідність лінійне перетворення 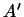 простору
простору 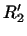 в
в 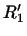 , Яке визначимо наступним чином.
, Яке визначимо наступним чином.
нехай 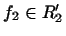 ,
, 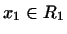 . Розглянемо
. Розглянемо 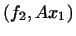 ; при фіксованому
; при фіксованому 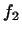 це лінійна функція від
це лінійна функція від 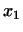 , Тобто може бути записана у вигляді
, Тобто може бути записана у вигляді 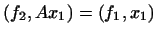 , де
, де 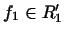 . Покладемо по визначенню
. Покладемо по визначенню 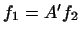 . отримується перетворення
. отримується перетворення 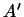 називається зв'язаним до
називається зв'язаним до 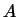 . Отже, якщо
. Отже, якщо 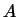 - лінійне перетворення простору
- лінійне перетворення простору 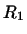 в
в 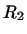 , То поєднане йому перетворення є лінійне перетворення
, То поєднане йому перетворення є лінійне перетворення 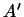 простору
простору 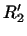 в
в 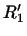 , Що задається тотожністю
, Що задається тотожністю
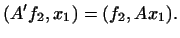
Встановимо одна важлива властивість операції переходу до парному перетворенню. нехай 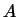 - лінійне перетворення простору
- лінійне перетворення простору 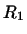 в
в 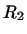 ,
, 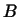 - лінійне перетворення простору
- лінійне перетворення простору 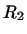 в
в 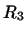 . позначимо через
. позначимо через 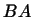 композицію цих перетворень, тобто лінійне перетворення простору
композицію цих перетворень, тобто лінійне перетворення простору 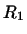 в
в 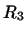 (за визначенням
(за визначенням 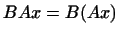 для будь-якого
для будь-якого 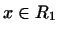 ).
).
Покажемо, що
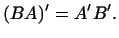
Справді, згідно з визначенням маємо: 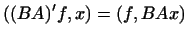 для будь-яких
для будь-яких 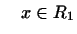 і
і 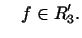 З іншого боку,
З іншого боку, 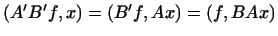 . Зіставляючи ці рівності, ми бачимо, що
. Зіставляючи ці рівності, ми бачимо, що 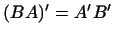 .
.
Вправа Довести, що лінійне перетворення, поєднане до 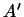 , є
, є 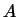 .
.
3 Взаємозамінність і.
У попередньому викладі  і
і  грали різну роль. Ми покажемо, що вони абсолютно рівноправні, тобто що все теореми залишаться справедливими, якщо ми поміняємо
грали різну роль. Ми покажемо, що вони абсолютно рівноправні, тобто що все теореми залишаться справедливими, якщо ми поміняємо  і
і  ролями.
ролями.
ми визначили  як сукупність лінійних функцій в
як сукупність лінійних функцій в  . Щоб встановити рівноправність
. Щоб встановити рівноправність  і
і  , Доведемо, що будь-яка лінійна функція
, Доведемо, що будь-яка лінійна функція 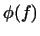 в
в  може бути записана у вигляді
може бути записана у вигляді 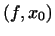 , де
, де 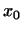 - фіксований вектор з
- фіксований вектор з  .
.
нехай  - деякий базис в
- деякий базис в  і
і 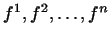 - взаємний з ним базис в
- взаємний з ним базис в  . лінійна функція
. лінійна функція 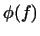 може бути записана у вигляді
може бути записана у вигляді
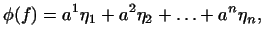
де 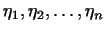 - координати вектора
- координати вектора 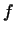 в базисі
в базисі 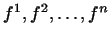 . Розглянемо вектор
. Розглянемо вектор 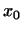 , Що має в базисі
, Що має в базисі  координати
координати 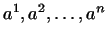 . Тоді, як ми бачили в п.2,
. Тоді, як ми бачили в п.2, 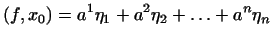 і, отже,
і, отже,
Ця формула встановлює взаємно однозначну відповідність між лінійними функціями 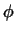 , Заданими в
, Заданими в  , І векторами
, І векторами 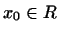 .
.
Ми можемо тому в усьому викладі вважати  простором лінійних функцій над
простором лінійних функцій над  , Задаючи ці лінійні функції формулою ( 5 ). Цим встановлено повну рівноправність між
, Задаючи ці лінійні функції формулою ( 5 ). Цим встановлено повну рівноправність між  і
і  .
.
Зауважимо, що при одночасному вивченні простору і сполученого простору ми вживаємо лише звичайні для векторів операції додавання і множення на число в кожному просторі і операцію 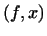 , Яка б пов'язала елементи обох просторів. Можна тому дати інше визначення пари сполучених просторів
, Яка б пов'язала елементи обох просторів. Можна тому дати інше визначення пари сполучених просторів  і
і  , При якому їх рівноправність безпосередньо видно. Це визначення полягає в наступному: ми розглядаємо пару
, При якому їх рівноправність безпосередньо видно. Це визначення полягає в наступному: ми розглядаємо пару 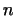 -мірних просторів
-мірних просторів  і
і  і кожній парі векторів
і кожній парі векторів 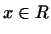 ,
, 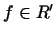 відносимо число
відносимо число 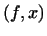 , Вимагаючи при цьому, щоб виконувалися умови 1
, Вимагаючи при цьому, щоб виконувалися умови 1 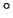 -4
-4 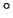 попереднього пункту і умова
попереднього пункту і умова
5 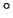 з
з 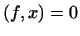 для будь-якого
для будь-якого 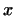 слід
слід 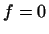 і із
і із 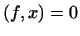 для будь-якого
для будь-якого 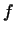 слід
слід 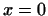 .
.
Коротко кажучи, пара сполучених просторів  і
і  - це пара
- це пара 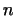 -мірних просторів з введеної додатково операцією
-мірних просторів з введеної додатково операцією 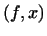 , Що задовольняє перерахованим умовам.
, Що задовольняє перерахованим умовам.
Зауваження У п.2 ми довели, що для кожного базису в  існує і притому єдиний взаємний з ним базис в
існує і притому єдиний взаємний з ним базис в  . З рівноправності між
. З рівноправності між  і
і  випливає, що для будь-якого базису в
випливає, що для будь-якого базису в  існує і притому єдиний взаємний з ним базис в
існує і притому єдиний взаємний з ним базис в  .
.
4 Перетворення координат в і.
Якщо ми розглядаємо координати векторів 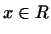 в деякому базисі
в деякому базисі  , То координати векторів
, То координати векторів 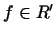 ми будемо, як правило, розглядати в базисі
ми будемо, як правило, розглядати в базисі 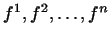 , Взаємне до базису
, Взаємне до базису  . перейдемо в
. перейдемо в  від базису
від базису  до нового базису
до нового базису 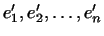 , і нехай
, і нехай
- формули цього переходу.
позначаючи через 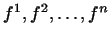 базис, взаємний з базисом
базис, взаємний з базисом  , А через
, А через 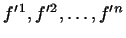 - базис, взаємний з базисом
- базис, взаємний з базисом 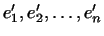 , Знайдемо матрицю
, Знайдемо матрицю 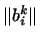 переходу від базису
переходу від базису  до базису
до базису 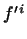 .
.
Знайдемо спочатку зворотну їй матрицю 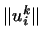 переходу від
переходу від 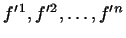 до
до 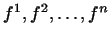 :
:
Для цього обчислимо двома способами вираження 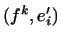 :
:
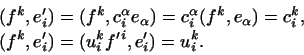
Звідси маємо 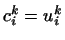 , Тобто матриця
, Тобто матриця 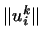 є транспонованою 5.1 до матриці переходу ( 6 ). Отже, матриця переходу
є транспонованою 5.1 до матриці переходу ( 6 ). Отже, матриця переходу
від 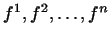 до
до 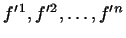 дорівнює матриці, транспонованою до матриці, зворотної матриці
дорівнює матриці, транспонованою до матриці, зворотної матриці 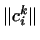 переходу від
переходу від  до
до 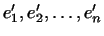 .
.
З'ясуємо тепер, як перетворюються координати векторів в  і в
і в  . нехай
. нехай 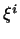 - координати вектора
- координати вектора 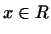 в базисі
в базисі  і
і 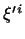 - його координати в новому базисі
- його координати в новому базисі 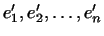 .
.
тоді
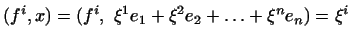
і 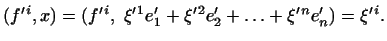 Тому
Тому 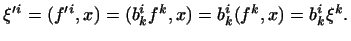 Отже,
Отже,
т. е координати векторів в  перетворюються за тими ж формулами, що і вектори взаємного базису в
перетворюються за тими ж формулами, що і вектори взаємного базису в  . Аналогічно, координати векторів в
. Аналогічно, координати векторів в  перетворюються за тими ж формулами, що і вектори взаємного базису в
перетворюються за тими ж формулами, що і вектори взаємного базису в  , Тобто
, Тобто
Ми можемо таким чином, сформулювати наступне правило: при переході від старої системи координат до нової об'єкти, що мають нижній індекс, перетворюються матрицею 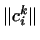 , Об'єкти, які мають верхній індекс, перетворюються матрицею
, Об'єкти, які мають верхній індекс, перетворюються матрицею 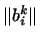 , Зворотного до
, Зворотного до 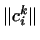 .
.
Той факт, що матриця 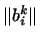 є зворотною до матриці
є зворотною до матриці 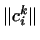 , Виражається співвідношеннями
, Виражається співвідношеннями
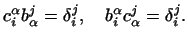
5 Простір, поєднане до евклидову.
Обмежимося для простоти евклідовому простором над полем дійсних чисел.
[Section] Для простоти розглядається евклідів простір над полем дійсних чисел
Лемма Нехай  є
є 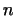 -мірним евклидово простір. Тоді кожну лінійну функцію в ньому можна записати у вигляді
-мірним евклидово простір. Тоді кожну лінійну функцію в ньому можна записати у вигляді
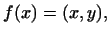
де 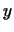 - фіксований вектор, однозначно визначається лінійною функцією
- фіксований вектор, однозначно визначається лінійною функцією 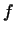 . Назад, кожен вектор
. Назад, кожен вектор 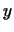 визначає лінійну функцію
визначає лінійну функцію 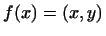 .
.
Доведення. виберемо в  деякий ортогональний нормований базис
деякий ортогональний нормований базис  . лінійна функція
. лінійна функція 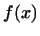 в цьому базисі може бути записана у вигляді
в цьому базисі може бути записана у вигляді
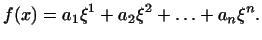
введемо вектор 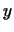 з координатами
з координатами 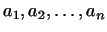 . Так як базис
. Так як базис  - прямокутний, то
- прямокутний, то
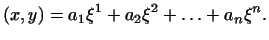
Ми довели, таким чином, існування такого вектора 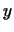 , Що для будь-якого
, Що для будь-якого 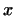 має місце рівність
має місце рівність 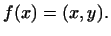
Доведемо тепер, що такий вектор визначається однозначно. нехай
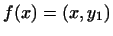
і 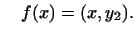 тоді
тоді 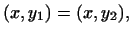 тобто
тобто 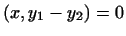 для будь-якого
для будь-якого 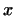 . отже,
. отже, 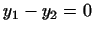 . Однозначність доведена.
. Однозначність доведена. 
Таким чином, в разі евклідового простору ми можемо кожен елемент 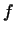 з
з  замінити відповідним елементом
замінити відповідним елементом 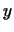 з
з  і при цьому замість
і при цьому замість 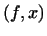 писати
писати 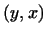 . Так як при одночасному вивченні простору і сполученого простору ми вживаємо лише звичайні для векторів операції і операцію
. Так як при одночасному вивченні простору і сполученого простору ми вживаємо лише звичайні для векторів операції і операцію 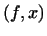 , Яка б пов'язала елементи
, Яка б пов'язала елементи 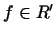 і
і 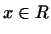 , То ми можемо в разі евклідового простору замінити
, То ми можемо в разі евклідового простору замінити 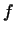 на
на 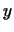 ,
,  на
на  і
і 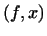 на
на 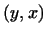 , Тобто ототожнити евклидово простір з парним до нього простором
, Тобто ототожнити евклидово простір з парним до нього простором  5.2 . Це висловлюють іноді і так: в евклідовому просторі можна замінити коваріантні вектори контраваріантнимі.
5.2 . Це висловлюють іноді і так: в евклідовому просторі можна замінити коваріантні вектори контраваріантнимі.
При такому ототожненні простору  і сполученого до нього простору
і сполученого до нього простору  поняття ортогональності векторів
поняття ортогональності векторів 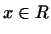 і
і 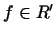 , Введене в пункті 2, переходить в звичайне для евклідового простору поняття ортогональності двох векторів з
, Введене в пункті 2, переходить в звичайне для евклідового простору поняття ортогональності двох векторів з  .
.
нехай  - довільний базис в
- довільний базис в  , а
, а 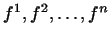 - взаємний з ним (біортогональний) базис в
- взаємний з ним (біортогональний) базис в  . Так як у випадку евклідового простору
. Так як у випадку евклідового простору  і
і  ототожнені, то ми можемо вважати вектори біортогональних до
ототожнені, то ми можемо вважати вектори біортогональних до 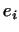 базису
базису 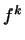 також векторами з
також векторами з  .
.
З'ясуємо, як нам знайти в цьому випадку по базису  базис
базис 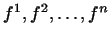 . висловимо спочатку
. висловимо спочатку 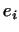 через
через 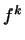 :
:
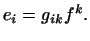
Нам потрібно знайти коефіцієнти 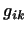 . Для цього помножимо скалярно обидві частини рівності на
. Для цього помножимо скалярно обидві частини рівності на 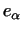 :
: 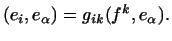
Так як, в силу взаємності (біортогональних) базисів 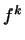 і
і 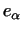 ,
,
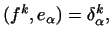
то 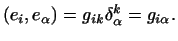
Отже, якщо базис 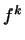 біортогонален до базису
біортогонален до базису 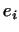 , то
, то
де матриця 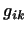 обчислюється за формулою
обчислюється за формулою 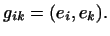
Звідси, дозволивши співвідношення ( 10 ) щодо  , Маємо:
, Маємо:
де  - матриця, обернена до
- матриця, обернена до 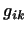 , Тобто
, Тобто 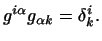
Вправа Показати, що
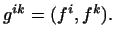





Next: 24 тензори Previous: 4 Поняття про тензори Vadim Yu.Radionov
2000-08-30
Подивитися коментарі
[2]