Основи тепло і масообміну для систем охолодження

1. Теплопровідність.
2. Теплопровідність металів і її зв'язок з електропровідністю
3. Теплопровідність кристалів.

Постійно стикаючись з нерозумінням основ теплообміну (тепломассообмена) серед займаються складанням теплопровідних складів, будівництвом систем охолодження, вважав за необхідне і корисним для читачів викласти тут основи тепло і масообміну.
Для розуміння процесів цього достатньо, але це треба знати, якщо Ви займаєтеся експериментами з теплопровідних складами і системами охолодження!

Тепло массообмен- розділ фізики, в якому розглядаються процеси перенесення теплоти (енергії) і маси (речовини).

Явища теплообміну пов'язані з необоротним перенесенням енергії з однієї частини простору в іншу і викликані різницею температур, а явища масообміну - з переміщенням речовини з однієї частини простору в іншу і викликані різницею концентрацій.

Якщо теплообмін і масообмін супроводжують один одного і їх доводиться розглядати у взаємозв'язку, то маємо справу з ТЕПЛОМАСООБМІННИХ.

Коли явища теплообміну і масообміну мало впливають один на одного, їх можна розглядати окремо. Іноді має місце тільки якусь одну явище. Відповідні процеси в цих випадках називають процесами теплообміну, масообміну.

Розрізняють три види перенесення енергії у вигляді теплоти:

Теплопровідність - молекулярний перенос теплоти - в суцільному середовищі, викликаний різницею температур.

Конвекція - процес перенесення теплоти при переміщенні макроскопічних об'ємів рідини або газу з області з одного температурою в область з іншого - при цьому перенесення теплоти нерозривно пов'язаний з переносом речовини.

Процеси конвекції супроводжуються теплопровідністю; цей спільний процес називається конвективним теплообміном.

Теплове випромінювання-процес перенесення теплоти, обумовлений перетворенням внутрішньої енергії речовини в енергію випромінювання - перенесенням її в вигляді електромагнітних хвиль і їх поглинанням речовиною.

Перенесення речовини відбувається за допомогою дифузії і конвективного масообміну.

Дифузія - молекулярний перенос речовини в середовищі, викликаний різницею концентрацій (концентраційна дифузія), температур (термодифузія) або давленій- (бародіффузія).

Конвективний массообмен - перенесення речовин, викликаний спільною дією конвективного перенесення речовини і молекулярної дифузії. Наведемо приклади, пов'язані з перенесенням теплоти і маси в природі:

Такі процеси, як випаровування сушка, утворення хмар, являють собою цілий комплекс явищ тепломасообміну, що супроводжуються фазовими перетвореннями.

2. З підвищенням температури збільшуються інтенсивність і частота руху молекул і атомів: тому теплопровідність буде збільшуватися з підвищенням температури

Згідно з теоріями тепла і будови речовини прийнято вважати, що теплопровідність в аморфних твердих тілах, рідинах і газах є результатом безпосереднього перенесення молекулярного (або атомного) руху від молекули до молекули в дотичних поверхнях. Цей спосіб теплообміну часто представляють як процес дифузії тепла. У речовинах з більш складною структурою, таких, наприклад, як кристали, руху атомів перетворюються в коливальні рухи всього каркаса кристала.

Відповідно до останніх даних теорії теплопровідності в твердих тілах проводять чітке розмежування між діелектриками (неметалами) і металами, таким чином ці речовини взагалі мають більш високу теплопровідність.

У діелектриках теплообмін здійснюється коливаннями атомів кристалічної решітки. Діелектрики можуть мати високу теплопровідність.

В металах і інших твердих провідниках електрики передача тепла здійснюється коливаннями кристалічної решітки і вільними електронами. Таким чином, ці речовини взагалі мають більшу теплопровідність.

Процеси фазових змін - від твердого тіла до рідини - припускають зміна від стану щодо впорядкованого розташування молекул до неупорядкованого стану. Ця зміна фази породжує істотні зміни в молекулярній будові.

Воно послаблює молекулярні зв'язки, порушує стан твердого тіла і створює можливість теплового руху молекул. Ці зміни призводять до висновку, що рідина може бути абсолютно подібна газу в тому відношенні, що молекули в рідині знаходяться повністю в хаотичному стані, але групуються на середніх міжмолекулярних відстанях, менших, ніж молекули газу

Цей висновок не є абсолютно безперечним, оскільки поблизу точки плавлення рідкий стан не може дуже відрізнятися від твердого і, отже, немає умов для вільного молекулярного руху. З цієї причини в основі сучасних теорій лежить положення, що будова рідин більш нагадує будову твердих тіл, ніж будова газів, і зберігає видимість порядку в більшій мірі. Це уявлення підтверджується такими експериментальними даними, як рентгенівські дифракційні вимірювання.

Процес випаровування послаблює міжмолекулярні зв'язки, які існують в рідинах, і збільшує міжмолекулярні відстані до такої міри, що молекули знаходять можливість вільного руху в будь-якому напрямку. Єдиною перешкодою на їх шляху можуть бути тільки інші молекули, з якими вони можуть зіткнутися. Газ поблизу будь кордону поверхні має випадковий розподіл молекул. В цьому випадку всі властивості і особливості газу можна пояснити кінетичної теорії газів. Іншими словами, теплопровідність в газах можна порівнювати з процесами, молекулярної дифузії від більш гарячих шарів до більш холодним, при цьому теплопровідність в газах обумовлюється обміном розташування і енергією молекул.

Існують і інші уявлення про фізичну сущносгі перенесення теплової енергії; проте в будь-якому випадку перенесення енергії пов'язують з теплом і процес перенесення енергій називають теплопровідністю.

Хоча навіть основний механізм теплопровідності неповністю ясний, але тим не менше гіпотези, на яких грунтується наука про теплопровідності, грунтуються на експериментальних спостереженнях.

Послідовне застосування цих гіпотез як основ для математичного аналізу, який подтверждаетсяексперіментальнимі даними, саме по собі вже досить, щоб встановити закон, що характеризує перенесення.
Встановлений таким чином основний закон повністю відповідає класичній термодинаміці. Все вищевказане в меншій мірі стосується фізичної природи теплопровідності і головним чином ілюструє застосування основного закону теплопровідності до теплопереносу в системах.

Згідно з другим законом термодинаміки тепло поширюється від одного тіла до іншого (або від однієї частини тіла до іншої частини того ж тіла), якщо існує різниця температур. При цьому потік тепла спрямований від точки з більшою температурою до точки з меншою температурою. Відповідно до першого закону термодинаміки (збереження енергії) потік теплової енергії зберігається при відсутності джерел тепла або стоків. Тому в твердому тілі має місце розподіл температур, яке залежить від просторових координат і часу спостереження:

Можна припускати, що в цьому випадку в твердому тілі є така поверхня, при спостереженні за якої в певний (часом опиниться, що все її точки мають однакову температуру. Така поверхня називається ізотермічної поверхнею.

Можна виявити інші ізотермічні поверхні всередині цього тіла, температури яких відрізняються від температури зазначеної поверхні на величину + δ t. Ці ізотермічні поверхні ніколи не перетинаються, так як ніяка точка, не існує в цьому твердому тілі при двох різних температурах в один і той же час. Таким чином, тверде тіло представляється нам як би складеним з певної кількості довільно тонких ізотермічних оболонок, які, звичайно, змінюються з часом.

Далі розглядаються тільки ізотропні тверді тіла, т. Е. Такі тверді тіла, (Властивості яких і їх структура в околиці будь-якої крапки не залежать від напрямку. В цьому випадку внаслідок симетрії потік тепла в точці обов'язково має напрямок, перпендикулярний до ізотермічної поверхні через точку. це положення буде обговорюватися нижче,

Математичне формулювання закону теплопровідності може бути виражена таким чином:

Рівняння (1) можна пояснити, скориставшись рис. 1. Потік тепла Q / А протікає по (перпендикуляру п) до площі А в напрямку зменшення температури, т. Е. В напрямку негативного градієнта температури. Знак мінуса в рівнянні (2-1) вказує на те, що потік тепла йде в бік негативного градієнта, і служить для того, щоб зробити потік тепла в цьому сенсі позитивним.

Мал. 1 До висновку закону теплопровідності.

Коефіцієнт пропорційності λ висловлює теплопровідність і є характеристикою матеріалу, через який проходить потік тепла.

Для нескінченно малої площадки, виділеної з площі, рівняння (1) можна записати у вигляді:

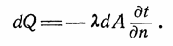
(2)

Рівняння (1) і (2) зазвичай приписуються французькому математику Жану Батісту Фур'є і в його честь названі рівняннями теплопровідності Фур'є ..

Кількість тепла, що проходить за годину через одиницю площі будь-якій поверхні, називається питомою потоком тепла q і вимірюється в ккал / м 2 • год або Вт / м2.

Потік тепла - вектор, іншими словами, він повинен характеризуватися як величиною, так і напрямком.

Тепловий потік може бути визначений уздовж будь-якого напрямку через площу, перпендикулярну цьому напрямку.

На рис. 2 показані ізотерми тіла t і tdt. Перпендикуляр до цих ізотермам позначений променем п, який є також перпендикуляром і до елементу площі dА, Потік тепла по перпендикуляру і в напрямку S можна обчислити таким чином:

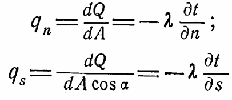
Легко показати, що n = s зі sα. Тому

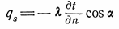
(3)

Або інакше, qs є складовою вектора теплового потоку q п.

З рівняння (3) випливає, що найбільшим потоком тепла буде той, який розрахований уздовж нормалі до ізотермічних поверхонь. Зокрема, якщо складові потоки відносяться до площин, які мають системи координат х, у, z, то це будуть потоки

(4)

Потоки, виражені рівнянням (4), є складовими вектора тепловогопотока.

Теплопровідність.

Слід зазначити, що коефіцієнт теплопровідності λ необов'язково повинен бути постійним. Насправді теплопровідність є функцією температури для всіх фаз, а в рідинах і газах залежить також від тиску, особливо поблизу до критичного стану. Теплопровідність в дереві і кристалах також помітно змінюється від напрямку. Так, наприклад, теплопровідність в дереві поперек волокна в порівнянні з теплопровідністю дерева вздовж волокна змінюється на множник від 2 до 4.

Залежність теплопровідності від температури для окремих невеликих діапазонів температури може бути прийнятно виражена в лінійному вигляді:

(5)

де: λ0 - величина теплопровідності при деяких початкових умовах, β- температурний коефіцієнт, він може бути позитивним або негативним в залежності від матеріалу.

Мал. 3 показує зміну температурного градієнта в тілі в залежності від того, позитивно чи негативно β.

Легко зрозуміти, що лінійний градієнт температури існує тільки при постійній теплопровідності.

Цікаво відзначити, що рівняння Фур'є для теплопровідності абсолютно аналогічно закону Ома для електричного провідника. Закон Ома для провідника будь-якої форми можна висловити так:

(6)

У рівнянні (6) електричний струм відповідає потоку тепла Q, електричний потенціал Е відповідає температурі I і електропровідність σ (σ = I / р, де ρ-електричний опір) відповідає теплопровідності.

Оскільки рівняння (2) і (6) мають один і той же вид, то температурне поле всередині нагрітого тіла і поле електричної напруги в тілах такої ж форми аналогічні за умови, що розподіл температур на поверхні відповідає поверхневому розподілу електричної напруги. Ця аналогія сприяє більш детальному з'ясуванню задач теплопровідності за допомогою подібних електричних ланцюгів.

У неорганічних, неметалічних, тугоплавких матеріалах (кераміка, природні кам'яні матеріали, бетони та ін.) Кількість вільних електронів, які могли б рухатися через кристалічну решітку і здійснювати перенесення енергії, недостатньо і теплота в основному передається за рахунок коливань решітки.

Величина теплопровідності залежить від характеру коливань решітки. При гармонійних коливаннях опір переносу енергії відсутній і теплопровідність може досягати величезних значень. Однак в реальних кристалах коливання мають ангармонічного характер, який сприяє часткового загасання пружних теплових коливань і значного зниження теплопровідності.

В теорії теплопровідності передбачається, що коливання нормального вигляду квантуються і по аналогії з фотонами в теорії світла ці кванти називають фононами, а механізм перенесення теплової енергії - фононної теплопровідністю.

Таким чином, у твердих неметалевих тел перенесення теплової енергії здійснюється за рахунок взаємодії фононів, в результаті їх руху, зіштовхування, розсіювання і т.п. За аналогією з кінетичної теорії газів фононну теплопровідність твердих тіл можна уявити як

де: l - довжина вільного пробігу фононів, з - питома теплоємність тіла, ν - середня швидкість фононів;

В металах перенесення теплової енергії визначається рухом і взаємодією електронів провідності, так як ґратчаста фононний складова теплопровідності зникаюче мала і

Явище перенесення тепла в напівпровідниках складніше, ніж в діелектриках і металах, так як для них істотні як решеточная, так і електронна складові теплопровідності. Крім того, тут теплопровідність залежить від теплопровідності домішок і багатьох інших факторів.

Теплопровідність - це перенесення теплової енергії структурними частинками речовини (молекулами, атомами, іонами) в процесі їх теплового руху. Такий теплообмін може відбуватися в будь-яких тілах з неоднорідним розподілом температур, але механізм перенесення теплоти буде залежати від агрегатного стану речовини. Явище теплопровідності полягає в тому, що кінетична енергія атомів і молекул, яка визначає температуру тіла, передається іншому тілу при їх взаємодії або передається з більш нагрітих областей тіла до менш нагрітих областей. Іноді теплопровідністю називається також кількісна оцінка здатності конкретної речовини проводити тепло.

Чисельна характеристика теплопровідності матеріалу дорівнює кількості теплоти, що проходить через матеріал товщиною 1 м і площею 1 кв. м за одиницю часу (секунду) при різниці температур на двох протилежних поверхнях в 1 К. Дана чисельна характеристика використовується для розрахунку теплопровідності для калібрування і охолодження профільних виробів.

Таблиця 1

Матеріал Теплопровідність,
Вт / (м · K) Матеріал Теплопровідність,
Вт / (м · K) Графен 4840 - 530 0 Кальцій 201 Алмаз 1001-2600 Вольфрам 173 Срібло 430 Магній 156 Мідь 382-390 Родий 150 Золото 320 Іридій 147 Алюміній 202-236 Молібден 138 Берилій 201 Рутеній 117 Латунь 97-111 Хром 93 , 9 Залізо 92 Осмий 87,6 Платина 70 Титан 21,9 Олово 67 Тефлон 0,25 Сталь 47 Водень (300к) 0,1815 Кварц кристал (25 ° С) 6,8 / 11,3 Папір 0,14 Кварц плавлений 1 , 38 Полістирол 0,082 Скло 1-1,15 Шерсть 0,05 КПТ-8 0,7 - 1 Мінеральна вата 0,045 Вода при нормальних умовах 0,6 Пінополістирол 0,04 Цегла будівельний 0,2-0,7 Скловолокно 0,036 Пінобетон 0, 14-0,3 Коркове дерево 0,035 дерево 0,15 Пінзеля 0,035 Свіжий сніг 0,10 0,15 Каучук спінений 0,03 Вата 0,055 Аргон 0,0177 Повітря (300 K, 100 кПа) 0,026 Аерогель 0,017 Вакуум (абсолютний) 0 (строго) Ксенон 0,0057

Теплопровідність Si (300 K) 149 Вт / (м · К)

Теплопровідність металів і її зв'язок з електропровідністю

Закон Видемана - Франца - це фізичний закон, який стверджує, що для металів відношення коефіцієнта теплопровідності (або тензора теплопровідності) K до питомої електричної провідності (або тензора провідності) σ пропорційно температурі:

або

де: k - постійна Больцмана, e - заряд електрона, T - температура.

Теплопровідність кристалів.

фонон

У кристалах і при низьких температурах слід враховувати квантовий характер теплових хвиль.

Якщо, ћω D << k B T то при теплообміні порушуються будь-які коливання в кристалі, всі квантові переходи можливі, і тому квантовий характер явища теплообміну не помітний.

При низьких температурах, коли ћω D >> k BT, в кристалі порушено лише коливання з малими частотами, і великі енергетичні сходинки не можуть бути подолані виникають тепловими «поштовхами». Розглянемо процес передачі тепла на основі уявлень про фонони.

З теорії Дебая слід, що збуджений стан решітки можна уявити як ідеальний газ фононів, що вільно рухається в обсязі кристала. Фононний газ в певному інтервалі температур поводиться подібно ідеальному газу, а оскільки фонони є основними переносниками тепла в твердому тілі (це твердження справедливе лише для діелектриків), то коефіцієнт теплопровідності твердого тіла можна виразити такою ж залежністю, як коефіцієнт теплопровідності ідеального газу

де: C '- теплоємність одиниці об'єму фононного газу, l ф - середня довжина вільного пробігу фонона, υ м - швидкість поширення звуку в даному тілі.

Обчислення середньої довжини вільного пробігу фонона являє собою складну задачу, оскільки вона залежить від того, на чому відбувається розсіювання фононів: на інших фононах, на дефектах структури або на зовнішніх гранях зразка. Однак теоретичний аналіз призводить до того, що при досить високих температурах середня довжина вільного пробігу фонона обернено пропорційна абсолютній температурі. Тому коефіцієнт теплопровідності твердих тіл при температурах вище характеристичною (T> Θ D) обернено пропорційний абсолютній температурі.

У досить чистих і бездефектних кристалах при температурі, близькій до абсолютного нуля, виникає залежність середньої довжини вільного пробігу фононів від розмірів зразка. Це пояснюється тим, що при низьких температурах концентрація фононів мала, а отже, мала ймовірність розсіювання фононів на інших фононах. Приклад залежності коефіцієнта теплопровідності від температури при різних перетинах зразка монокристалла LiF показаний на рис. 6.10 [98]. Видно, що відмінність в теплопровідності для зразків різного перетину проявляється тільки в області низьких температур.

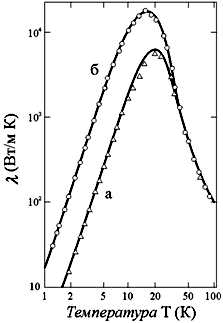
Мал. 4 граткову (фононний) теплопровідність як функція від температури для монокристала LiF при його різних перетинах:
а - 1,33 х 0,91 мм; б - 7,55 х 6,97 мм

Вважаючи середню довжину вільного пробігу фононів приблизно рівною лінійними розмірами кристала ((l ф) ~ L, де L - лінійний розмір кристала), можна рівняння (7) переписати у вигляді:

У правій частині рівняння (8) від температури залежить тільки теплоємність одиниці об'єму фононного газу C '. При температурах, близьких до абсолютного нуля, теплоємність пропорційна T 3 (закон T 3 Дебая), тому і коефіцієнт теплопровідності l пропорційний кубу абсолютної температури. Такий висновок підтверджується експериментальними даними.

Анізотропія сил зв'язку в кристалах приводить до анізотропії коефіцієнта теплопровідності. Це можна проілюструвати на прикладі монокристалла кварцу (рис. 5). У табл. 2 представлені дані про коефіцієнт теплопровідності у напрямку, паралельному осі с, і по перпендикулярному до цієї осі напрямку.

Теплопровідність кристала кварцу з різних напрямків (одиниці λ - Вт / (м * К) за даними Л.3 гл.6-5

Таблиця 2

Напрямок Температура, ° C 100 0 -78 -100 Паралельно осі з 3,223 4,898 7,032 17,623 Перпендикулярно осі з 2,009 2,595 3,642 8,832

З даних таблиці 2 видно, що коефіцієнт теплопровідності уздовж гексагональної осі з кварцу приблизно вдвічі вище відповідних значень в напрямках перпендикулярних осі с, тобто в напрямках, що лежать в базисної площини кристала. Зі зниженням температури коефіцієнт теплопровідності зростає, як і передбачає квантова теорія.

Все вищесказане відноситься до решеточной (фононної) частини теплоємності твердого тіла, властивої неметаллическим кристалів. В металах в перенесенні тепла, крім атомів кристалічної решітки, беруть участь ще й вільні електрони, які одночасно є і носіями електричного заряду, забезпечуючи високу електропровідність металів. Більш того, в чистих металах основними носіями тепла є саме вільні електрони, а не фонони. При досить високих температурах металів решеточная складова теплопровідності становить всього 1-2% від електронної теплопровідності. Цим пояснюється висока теплопровідність чистих металів в порівнянні з діелектриками. Наприклад, у алюмінію при кімнатній температурі коефіцієнт теплопровідності l = 2,26х106 Вт / (смхК), що приблизно на два порядки більше, ніж у кварцу (див. Табл. 1). Однак при дуже низьких температурах в металах електронна частина теплопровідності менше, ніж решеточная. Це пояснюється ефектами електрон-фононного розсіювання.

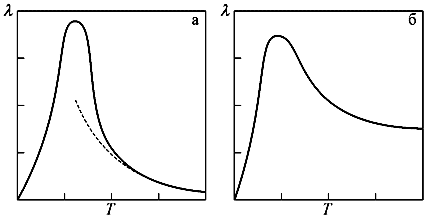
На рис. 6 наведено вид залежності теплопровідності від температури для діелектриків і металів.

Мал. 6 Порівняльні температурні залежності коефіцієнта теплопровідності l: а - для діелектриків; б - для металів

У діелектриках, практично не мають вільних електронів, перенесення тепла здійснюється тільки фононами. Вище було сказано, що середня довжина вільного пробігу (l ф) залежить від процесів розсіювання фононів на різних об'єктах. Все це призводить до того, що температурна залежність коефіцієнта теплопровідності l для діелектриків має вигляд кривої з максимумом (рис. 6, а). Ліва висхідна гілка залежності обумовлена ​​збільшенням числа фононів з ростом температури, а права спадна пов'язана з ослабляють фонон-фононною і іншими видами розсіювання. Вид залежності l (T) для металів (рис. 6, б) якісно схожий на криву для діелектриків. Це пов'язано з переважанням при дуже низьких температурах фононного механізму теплопередачі. Однак зі зростанням температури внесок фононної складової в цей процес стає дуже малий і теплопередача здійснюється в основному вільними електронами.

При відносно високих температурах в металах коефіцієнт теплопровідності l практично перестає змінюватися зі збільшенням Т.

Мал. 7. Теплопровідність окремих матеріалів в широкому діапазоні температур

У табл. 1 і на рис. 7 показані значення коефіцієнтів теплопровідності для окремих матеріалів. Проблема тепловідводу для деяких мікроелектронних та оптоелектронних виробів є однією з ключових, що забезпечують їх надійність. Так, наприклад, для напівпровідникових лазерів, що працюють в режимі безперервної генерації, ця проблема є основною. З даних табл. 1 і рис. 7 випливає, що для поліпшення тепловідводу кристали можна кріпити на алмазні підкладки або підкладки з карбіду кремнію (як непровідні) або на підкладки срібні або мідні (як провідні).

У зв'язку із зростанням ступеня інтеграції і зменшенням геометричних розмірів елементів, в тому числі струмопровідних доріжок, з значень табл. 1 випливає, що єдиною альтернативою алюмінієвої металізації є використання міді. Срібло, хоча і володіє більш високим значенням теплопровідності, не може бути використано при металізації внаслідок високих значень коефіцієнта дифузії.

література:

1. Е.З. Еккерт, Р.М.Дрейк, Теорія тепло-і масообміну, пер. з англ. Під ред А.В. Ликова, ДЕІ, Москва
2. Г.Н. Дульнев, Тепло- та масообмін в радіоелектронній апаратурі, М, Вища школа, 1984,
3. Гуртів В.А., Осауленко Р.Н., гущевих К.В. Фізика твердого тіла для інженерів, http://dssp.petrsu.ru/files/tutorial/ftt/giv.htm , Глава 6.5 http://dssp.petrsu.ru/files/tutorial/ftt/Part6/part6_5.htm
4. Теплопередача, збірник формул, http://edu.delfa.net/CONSP/mkt8.html

Зібрав А.Сорокін жовт. 2011 р