моделювання фізичне

Модел і вання фіз і чеський, вид моделювання, який полягає в заміні вивчення деякого об'єкту або явища експериментальним дослідженням його моделі , Що має ту ж фізичну природу.

В науці будь-який експеримент, вироблений для виявлення тих чи інших закономірностей досліджуваного явища або для перевірки правильності і меж застосування знайдених теоретичним шляхом результатів, по суті являє собою моделювання, т. К. Об'єктом експерименту є конкретна модель, що володіє необхідними фізичними властивостями, а в ході експерименту повинні виконуватися основні вимоги, що пред'являються до М. ф. У техніці М. ф. використовується при проектуванні та спорудженні різних об'єктів для визначення на відповідних моделях тих чи інших властивостей (характеристик) як об'єкта в цілому, так і окремих його частин. До М. ф. вдаються не тільки з економічних міркувань, а й тому, що натурні випробування дуже важко або взагалі неможливо здійснити, коли дуже великі (малі) розміри натурного об'єкта або значення інших його характеристик (тиску, температури, швидкості протікання процесу і т. п.).

В основі М. ф. лежать подібності теорія і размерностей аналіз . Необхідними умовами М. ф. є геометрична подібність (подібність форми) і фізична подібність моделі і натури: в подібні моменти часу і в подібних точках простору значення змінних величин, що характеризують явища для натури, повинні бути пропорційні значенням тих же величин для моделі. Наявність такої пропорційності дозволяє виробляти перерахунок експериментальних результатів, одержуваних для моделі, на натуру шляхом множення кожної з визначених величин на постійний для всіх величин даної розмірності множник - коефіцієнт подібності.

Оскільки фізичні величини пов'язані певними співвідношеннями, витікаючими із законів і рівнянь фізики, то, вибравши деякі з них за основні, можна коефіцієнти подібності для всіх інших похідних величин виразити через коефіцієнти подібності величин, прийнятих за основні. Наприклад, в механіці основними величинами вважають зазвичай довжину l, час t і масу m. Тоді, оскільки швидкість v = l / t, коефіцієнт подібності швидкостей k v = v н / v м (індекс «н» у величин для натури, «м» - для моделі), можна висловити через коефіцієнти подібності довжин k l = l н / l м і часів k t = t н / t м у вигляді k v = k l / k t. Аналогічно, т. К. На підставі другого закону Ньютона сила F пов'язана з прискоренням w співвідношенням F = mw, то k F = k m × k w (де, в свою чергу, k w = k v / k t) і т. д. З наявності таких зв'язків витікає, що для даного фізичного явища деякі безрозмірні комбінації величин, що характеризують це явище, повинні мати для моделі і натури одне і те ж значення. Ці безрозмірні комбінації фізичних величин називаються критеріями подібності. Рівність всіх критеріїв подібності для моделі і натури є необхідною умовою М. ф. Однак домогтися цього рівності можна не завжди, т. К. Не завжди вдається одночасно задовольнити всім критеріям подібності.

Найчастіше до М. ф. вдаються при дослідженні різних механічних (включаючи гидроаеромеханике і механіку деформованого твердого тіла), теплових і електродинамічних явищ. При цьому число і вид критеріїв подібності для кожного модельованого явища залежить від його природи і особливостей. Так, наприклад, для завдань динаміки точки (або системи матеріальних точок), де все рівняння витікають з другого закону Ньютона, критерієм подібності є число Ньютона Ne = Ft 2 / ml і умова М. полягає в тому, що

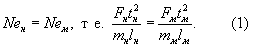
Для коливань вантажу під дією сили пружності F = cl рівність (1) призводить до умови t 2н з н / m н = t 2м з м / m м, що, наприклад, дозволяє по періоду коливань моделі визначити період коливань натури; при цьому явище не залежить від лінійного масштабу (від амплітуди коливань). Для руху в полі тяжіння, де F = km / l 2, умовою подібності є k н t 2н / l 3Н = k м t 2м / l 3м (явище не залежить від мас). При русі в одному і тому ж полі тяжіння, наприклад Сонця, k м = k н, і отримане співвідношення дає третій закон Кеплера для періоду звернення. Звідси, вважаючи одну з планет «моделлю», можна, наприклад, знайти період обертання, будь-який інший планети, знаючи її відстань від Сонця.

Для безперервного середовища при вивченні її руху число критеріїв подібності зростає, що часто значно ускладнює проблему М. ф. У гидроаеромеханике основними критеріями подібності є Рейнольдса число Re , Маху число М , Фруда число Fr , Ейлера число Еu , А для нестаціонарних (залежних від часу) течій ще і Струхаля число St . При М. ф. явищ, пов'язаних з перенесенням тепла в рухомих рідинах і газах або з физико-хімічними перетвореннями компонентів газових потоків та ін., необхідно враховувати ще ряд додаткових критеріїв подібності.

Створювані для гідроаеродинамічні моделювання експериментальні установки і самі моделі повинні забезпечувати рівність відповідних критеріїв подібності у моделі і натури. Зазвичай це вдається зробити у випадках, коли для течії в силу його особливостей зберігається лише один критерій подібності. Так, при М. ф. стаціонарного течії нестисливої в'язкої рідини (газу) визначальним буде параметр Re і необхідно виконати одну умову

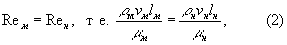
де r - щільність, m - динамічний коефіцієнт в'язкості середовища. При зменшеній моделі (l м <l н) це можна зробити, або збільшуючи швидкість (v м> v н), або використовуючи для моделювання іншу рідину, у якій, наприклад, r м> r н, а m м £ m н. При аеродинамічних дослідженнях збільшувати Vм в цьому випадку не можна (порушиться умова несжимаемости), але можна збільшити r м, використовуючи аеродинамічні труби закритого типу, в яких циркулює стиснене повітря.

Коли при М. ф. необхідно забезпечити рівність декількох критеріїв, виникають значні труднощі, часто непереборні, якщо тільки не робити модель тотожною натурі, що фактично означає перехід від М. ф. до натурних випробувань. Тому на практиці нерідко вдаються до наближеного моделювання, при якому частина процесів, що грають другорядну роль, або зовсім не моделюється, або моделюється приблизно. Таке М. ф. не дозволяє знайти прямим перерахунком значення тих характеристик, які не відповідають умовам подібності, і їх визначення вимагає відповідних додаткових досліджень. Наприклад, при М. ф. сталих течій в'язких стисливих газів необхідно забезпечити рівність критеріїв Re і М і безрозмірного числа c = cp / cv (cp і cv - питомі теплоємності газу при постійному тиску і постійному об'ємі відповідно), що в загальному випадку зробити неможливо. Тому, як правило, забезпечують для моделі і натури лише рівність числа М, а вплив на які визначаються параметри відмінностей в числах Re і c досліджують окремо або теоретично, або за допомогою інших експериментів, змінюючи в них в досить широких межах значення Re і c.

Для твердих тіл, що деформуються особливості М. ф. теж залежать від властивостей цих тіл і характеру розглянутих задач. Так, при моделюванні рівноваги однорідних пружних систем (конструкцій), механічні властивості яких визначаються модулем пружності (модулем Юнга) Е і безрозмірним Пуассона коефіцієнтом n, повинні виконуватися 3 умови подібності:

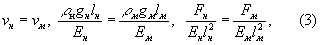
де g - прискорення сили тяжіння (g = r g - питома вага матеріалу). У природних умовах g м = g н = g, і отримати повне подобу при l м ¹ lн можна, лише підібравши для моделі спеціальний матеріал, у якого r м, Е м і n м задовольнятимуть першим двом з умов (3), що практично зазвичай нездійсненно.

У більшості випадків модель виготовляється з того ж матеріалу, що і натура. Тоді r м = r н, Е м = Е н і друга умова дає g м l м = g н l н. Коли вагові навантаження істотні, для виконання цієї умови вдаються до т. Зв. відцентровому моделюванню, т. е. поміщають модель у відцентрову машину, де штучно створюється приблизно однорідне силове поле, що дозволяє отримати g м> g н і зробити l м <l н. Якщо ж основними є інші навантаження, а вагою конструкції і, отже, обліком її питомої ваги g = r g можна знехтувати, то наближене М. ф. здійснюють при g м = g н = g, задовольняючи лише останньому із співвідношень (3), яке дає F м / l 2м = F н / l 2н, отже, навантаження на модель повинні бути пропорційні квадрату її лінійних розмірів. Тоді модель буде подібна натурі і якщо, наприклад, модель руйнується при навантаженні F кр, то натура руйнується при навантаженні F кр l н / l м. Неврахування в цьому випадку вагових навантажень дає наступне. Оскільки ці навантаження мають значення g l 3, а останнє з умов (3) вимагає пропорційності навантажень Р, то при l м <l н вагове навантаження на модель буде менше необхідної цією умовою, т. Е. М. ф. не буде повним і модель, як недовантажених, буде міцніше натури. Ця обставина теж можна врахувати або теоретичним розрахунком або додатковими експериментами.

Одним з видів М. ф., Що застосовуються до твердих деформується тіл, є поляризационно-оптичний метод дослідження напруг, заснований на властивості ряду ізотропних прозорих матеріалів ставати під дією навантажень (т. е. при деформації) анізотропними, що дозволяє досліджувати розподіл напружень в різних деталях за допомогою їх моделей з прозорих матеріалів.

При М. ф. явищ в інших безперервних середовищах відповідно змінюються вигляд і число критеріїв подібності. Так, для пластичних і в'язкопластичних середовищ в число цих критеріїв поряд з параметрами Фруда, Струхаля і модифікованим параметром Рейнольдса входять параметри Лагранжа, Стокса, Сен-Венана і т. Д.

При вивченні процесів теплообміну теж широко використовують М. ф. Для випадку перенесення тепла конвекцією визначальними критеріями подібності є Нуссельта число Nu = a l / l, Прандтля число Pr = n / a, Грасхофа число Gr = b gl 3 D T / n 2, а також число Рейнольдса Re, де a - коефіцієнт тепловіддачі, а коефіцієнт температуропровідності, # - коефіцієнт теплопровідності середовища (рідини, газу), n - кінематичний коефіцієнт в'язкості, b - коефіцієнт об'ємного розширення, D Т - різниця температур поверхні тіла і середовища. Зазвичай метою М. ф. є визначення коефіцієнта тепловіддачі, що входить в критерій Nu, для чого дослідами на моделях встановлюють залежність Nu від інших критеріїв. При цьому в разі вимушеної конвекції (наприклад, теплообмін при русі рідини в трубі) стає несуттєвим критерій Gr, а в разі вільної конвекції (теплообмін між тілом і яка покоїться середовищем) - критерій Re. Однак до значних спрощень процесу М. ф. це не призводить, особливо з-за критерію Pr, що є фізичною константою середовища, що при виконанні умови Pr м = Pr н практично виключає можливість використовувати на моделі середу, відмінну від натурної. Додаткові труднощі вносить і те, що фізичні характеристики середовища залежать від її температури. Тому в більшості практично важливих випадків виконати всі умови подібності не вдається; доводиться удаватися до наближеного моделювання. При цьому відмовляються від умови рівності критеріїв, мало впливають на процес, а ін. Умовам (наприклад, подібність фізичних властивостей середовищ, що беруть участь в теплообміні) задовольняють лише в середньому. На практиці часто використовують також т. Н. метод локального теплового моделювання, ідея якого полягає в тому, що умови подібності процесів для моделі і натури виконуються тільки в тій області моделі, де досліджується процес теплообміну. Наприклад, при дослідженні тепловіддачі в системі однотипних тіл (куль, труб) в теплообміні на моделі може брати участь лише одне тіло, на якому виконують вимірювання, а інші служать для забезпечення геометричної подоби моделі і натури.

У випадках перенесення тепла теплопровідністю (Кондукцией) критеріями подібності є Фур'є число Fo = at 0 / l 2 і число Біо Bi = a l / l, де t 0 - характерний проміжок часу (наприклад, період). Для апериодических процесів (нагрівання, охолодження) t 0 зазвичай відсутній і параметр Fo випадає, а відношення at / l 2 визначає безрозмірний час. При М. ф. таких процесів теплообміну вдається в широких межах змінювати не тільки розміри моделі, а й темп протікання процесу.

Проте частіше для дослідження процесів перенесення тепла теплопровідністю застосовують моделювання аналогове .

Електродинамічне моделювання застосовується для дослідження електромагнітних і електромеханічних процесів в електричних системах. Електродинамічна модель являє собою копію (в певному масштабі) натурної електричної системи зі збереженням фізичної природи основних її елементів. Такими елементами моделі є синхронні генератори, трансформатори, лінії передач, первинні двигуни (турбіни) і навантаження (споживачі електричної енергії), але число їх зазвичай значно менше, ніж у натурної системи. Тому і тут моделювання є наближеним, причому на моделі по можливості повно представляється лише досліджувана частина системи.

Особливий вид М. ф. заснований на використанні спеціальних пристроїв, що поєднують фізичні моделі з натурними приладами. До них відносяться стенди випробувальні для випробування машин, наладки приладів і т. п., тренажери для тренування персоналу, якого навчають управлінню складними системами або об'єктами, імітатори, що використовуються для дослідження різних процесів в умовах, відмінних від звичайних земних, наприклад при глибокому вакуумі або дуже високому тиску, при перевантаженнях і т. п. (див. барокамера , Космічного польоту імітація ).

М. ф. знаходить численні застосування як при наукових дослідженнях, так і при вирішенні великого числа практичних завдань в різних областях техніки. Їм широко користуються в будівельній справі (визначення втомних напруг, експлуатаційних руйнувань, частот і форм вільних коливань, віброзахист і сейсмостійкість різних конструкцій і ін.); в гідравліки і в гідротехніки (визначення конструктивних і експлуатаційних характеристик різних гідротехнічних споруд, умов фільтрації в грунтах, моделювання течій річок, хвиль, припливів і відливів і ін.); в авіації, ракетній і космічній техніці (визначення характеристик літальних апаратів та їх двигунів, силового й теплового впливу середовища і ін.); в суднобудуванні (визначення гідродинамічних характеристик корпусу, керма і судноплавних двигунів, ходових якостей, умов спуску і ін.); в приладобудуванні; в різних областях машинобудування, включаючи енергомашинобудування і наземний транспорт; в нафто- і газовидобутку, в теплотехніці при конструюванні і експлуатації різних теплових апаратів; в електротехніці при дослідженнях всіляких електричних систем і т. п.

Літ .: Седов Л. І., Методи подібності і розмірності в механіці, М., 1972; Гухман А. А., Введення в теорію подібності, М., 1963; Ейгенсон Л. С., Моделювання, М., 1952; Кирпичов М. В., Міхєєв М. А., Моделювання теплових пристроїв, М. - Л., 1936; Шнейдер П. Дж., Інженерні проблеми теплопровідності, пров. з англ., М., 1960; Віників В. А., Іванов-Смоленський А. В., Фізичне моделювання електричних систем, М. - Л., 1956.

С. М. Тарг, С. Л. Вишневецький, В. А. Арутюнов.