ЄДІ формули, шпаргалки - Диференціювання функцій комплексного змінного.
- Умови Коші - Рімана.
- Калькулятори з алгебри
- математичні калькулятори
- Алгебра 6,7,8,9,10,11 клас, ЄДІ, ДПА
Умови Коші - Рімана.
Щоб однозначна в області G функція комплексного змінного була аналітичної в G, необхідно і достатньо, щоб її дійсна і уявна частини були диференційованими функціями як функції двох дійсних змінних і задовольняли умовам Коші - Рімана в області G:
в декартових координатах: 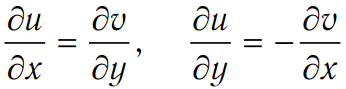 ,
,
в полярних координатах:  .
.
Функція f (z), диференційована в деякій області G, є аналітичною в цій області. З дифференцируемости функції в точці z 0 годі було її аналітичність в цій точці.
Правила обчислення похідних функцій комплексного змінного формально збігаються з правилами обчислення похідних для функцій дійсної змінної.
Калькулятори з алгебри
Рішення, підказки та підручник лінійної алгебри онлайн (всі калькулятори з алгебри). Калькулятори з алгебри
математичні калькулятори
Математичні калькулятори: коріння, дробу, степеня і рівняння, фігури, системи числення та інші калькулятори. математичні калькулятори
Алгебра 6,7,8,9,10,11 клас, ЄДІ, ДПА
Основна інформація за курсом алгебри для навчання і підготовки в іспитів, ГВЕ, ЄДІ, ОГЕ, ДПА Алгебра 6,7,8,9,10,11 клас, ЄДІ, ДПА