Тема 1.10. Обертання тіла навколо нерухомої осі

§1. Рух тіла по колу з постійною за модулем швидкістю

Рух тіла по колу з постійною за модулем швидкістю - це рух, при якому тіло за будь-які рівні проміжки часу описує однакові дуги.

Положення тіла на колі визначається радіусом-вектором 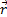, Проведеним з центру кола. Модуль радіуса-вектора дорівнює радіусу кола R (рис. 1).

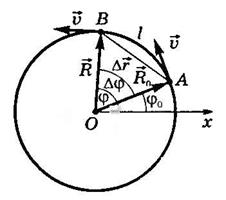
Рис.1. Рухи тіла по колу

За час Δt тіло, рухаючись з точки А в точку В, робить переміщення 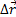, Рівне хорді АВ, і проходить шлях, рівний довжині дуги l.

Радіус-вектор повертається на кут Δφ. Кут висловлюють в радіанах.

швидкість 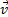руху тіла по траєкторії (кола) спрямована по дотичній до траєкторії. Вона називається лінійною швидкістю. Модуль лінійної швидкості дорівнює відношенню довжини дуги кола l до проміжку часу Δt, за який ця дуга пройдена: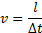

Скалярна фізична величина, чисельно рівна відношенню кута повороту радіуса-вектора до проміжку часу, за який цей поворот стався, називається кутовою швидкістю: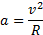

В СІ одиницею кутової швидкості є радіан в секунду .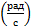

При рівномірному русі по колу кутова швидкість і модуль лінійної швидкості - величини постійні: ω = const; v = const.

Положення тіла можна визначити, якщо відомий модуль радіуса- вектора 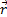і кут φ, який він складає з віссю Про х (кутова координата). Якщо в початковий момент часу t0 = 0 кутова координата дорівнює φ0, а в момент часу t вона дорівнює φ, то кут повороту Δφ радіуса-вектора за час Δt = t-t0 дорівнює Δφ = φ-φ0. Тоді з останньої формули можна отримати кінематичне рівняння руху матеріальної точки по колу: φ = φ 0 + ωt

Воно дозволяє визначити положення тіла в будь-який момент часу t.

Враховуючи що 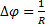, Отримуємо: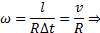

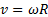- формула зв'язку між лінейнойі кутовий швидкістю.

Проміжок часу Т, протягом якого тіло робить один повний оберт, називається періодом обертання: 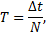де N - число оборотів, скоєних тілом за час Δt.

За час Δt = Т тіло проходить шлях l = 2πR. отже,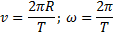

Величина θ, зворотна періоду, що показує, скільки оборотів здійснює тіло за одиницю часу, називається частотою обертання:

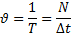
отже, .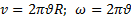

§2. Прискорення при русі тіла по колу з постійною за модулем швидкістю (доцентрове прискорення)

При рівномірному обертанні по колу модуль швидкості руху тіла не змінюється, але напрямок швидкості змінюється безперервно. Отже, даний рух - рух з прискоренням. Воно характеризує швидкість зміни швидкості у напрямку.

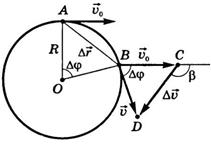
Рис.2. Рівномірний рух тіла по колу

прискорення 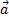направлено по радіусу до центру і тому називається доцентровим прискоренням: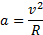

модуль 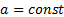, напрямок 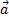безперервно змінюється (рис. 3). Тому дане рух не є рівноприскореному.

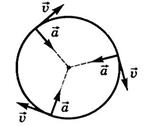
Рис.3. Напрямок центростремительного прискорення

§3. Обертальний рух твердого тіла навколо осі. Кутова швидкість і кутове прискорення

Для кінематичного опису обертального руху абсолютно твердого тіла навколо нерухомої осі використовуються ті ж величини, що і для опису руху матеріальної точки по колу.

Обертальнимрухом твердого тіла навколо нерухомої осі називається таке його рух, при якому будь-які дві точки, що належать тілу (або незмінно з ним пов'язані), залишаються в усі час руху нерухомими (рис.4).

Проміжок часу, протягом якого тіло робить один повний оберт навколо осі, - період обертання (Т). Величина, зворотна періоду, - частота обертання (ν).

Що проходить через нерухомі точки А і В пряма АВ називається віссю обертання.

Так як відстані між точками твердого тіла повинні залишатися незмінними, то очевидно, що при обертальному русі всі точки, що належать осі обертання, залишаться нерухомими, а всі інші точки тіла будуть описувати кола, площини яких перпендикулярні осі обертання, а центри лежать на цій осі.

Для визначення положення тіла, що обертається проведемо через вісь обертання, уздовж якої направимо вісь Az, напівплощина - нерухому і напівплощина, врізану в саме тіло і обертається разом з ним (рис. 4).

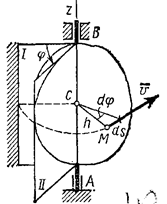
Рис.4. Обертальний рух тіла

Тоді положення тіла в будь-який момент часу однозначно визначиться узятим з відповідним знаком кутом φ між цими напівплощиною, який назвемо кутом повороту тіла. Будемо вважати кут φ позитивним, якщо він відкладений від нерухомої площини в напрямку проти годинникової стрілки (для спостерігача, що дивиться з позитивного кінця осі Az), і негативним, якщо по ходу годинникової стрілки. Вимірювати кут φ будемо завжди в радіанах. Щоб знати положення тіла в будь-який момент часу, треба знати залежність кута φ від часу t, тобто φ = f (t).

Рівняння виражає закон обертального руху твердого тіла навколо нерухомої осі.

При обертальному русі абсолютно твердого тіла навколо нерухомої осі кути повороту радіуса-вектора різних точок тіла однакові.

Основними кінематичними характеристиками обертального руху твердого тіла є його кутова швидкість ω і кутове прискорення ε.

Якщо за проміжок часу Δ t = t 1 - t тіло здійснює поворот на кут Δφ = φ 1 - φ, то чисельно середньої кутовий швидкістю тіла за цей проміжок часу буде 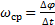. У межі при Δ t → 0 знайдемо, що

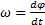або ω = .

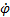Таким чином, числове значення кутової швидкості тіла в даний момент часу дорівнює першої похідної від кута повороту за часом. Знак ω визначає напрямок обертання тіла. Легко бачити, що коли обертання відбувається проти годинникової стрілки, ω> 0, а коли по ходу годинникової стрілки, то ω <0.

Розмірність кутової швидкості 1 / Т (тобто 1 / час); в якості одиниці вимірювання зазвичай застосовують рад / с або, що теж, 1 / с (з-1), так як радіан - величина безрозмірна.

Кутову швидкість тіла можна зобразити у вигляді вектора 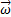, Модуль якого дорівнює | 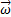| і який спрямований уздовж осі обертання тіла в ту сторону, звідки обертання видно, що відбувається проти годинникової стрілки (рис.5). Такий вектор визначає відразу і модуль кутової швидкості, і вісь обертання, і напрямок обертання навколо цієї осі.

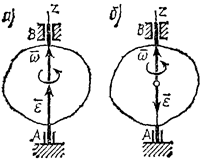
Рис.5. Напрямок кутової швидкості

Кут повороту і кутова швидкість характеризують рух всього абсолютно твердого тіла в цілому. Лінійна швидкість будь-якої точки абсолютно твердого тіла пропорційна відстані точки від осі обертання:

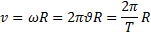
При рівномірному обертанні абсолютно твердого тіла кути повороту тіла за будь-які рівні проміжки часу однакові, тангенціальні прискорення у різних точок тіла відсутні, а нормальне прискорення точки тіла залежить від її відстані до осі обертання:

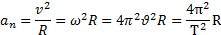
вектор 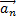спрямований по радіусу траєкторії точки до осі обертання.

Кутове прискорення характеризує зміну з плином часу кутової швидкості тіла. Якщо за проміжок часу Δ t = t 1 - t кутова швидкість тіла змінюється на величину Δω = ω 1 - ω, то числове значення середнього кутового прискорення тіла за цей проміжок часу буде 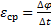. У межі при Δ t → 0 знайдемо,

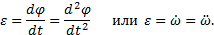
Таким чином, числове значення кутового прискорення, тіла в даний момент часу дорівнює першої похідної від кутової швидкості або другій похідній від кута повороту тіла за часом.

Розмірність кутового прискорення 1 / T 2 (1 / час 2); в якості одиниці вимірювання зазвичай застосовується рад / с2 або, що те ж, 1 / с2 (с2).

Якщо модуль кутової швидкості з часом зростає, обертання тіла називається прискореним, а якщо зменшується, - уповільненим. Легко бачити, що обертання буде прискореним, коли величини ω і ε мають однакові знаки, і уповільненим, - коли різні.

Кутове прискорення тіла (по аналогії з кутовий швидкістю) можна також зобразити у вигляді вектора ε, спрямованого уздовж осі обертання. При цьому

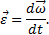
Напрямок ε збігається з напрямком ω, коли тіло обертається прискорено і (рис.5, а), протилежно ω при уповільненому обертанні (рис.5, б).