інтегральне числення

Интегр а льно исчисл е ня, розділ математики, в якому вивчаються властивості і способи обчислення інтегралів та їх застосування. І. і. тісно пов'язане з диференціальним численням і становить разом з ним одну з основних частин математичного аналізу (або аналізу нескінченно малих). Центральними поняттями І. і. є поняття певного інтеграла і невизначеного інтеграла функцій одного дійсного змінного.

Визначений інтеграл. Нехай потрібно обчислити площу S «криволінійної трапеції» - фігури ABCD (див. Рис.), Обмеженою дугою безперервної лінії, рівняння якої в = f (x), відрізком AB осі абсцис і двома координатами AD і BC. Для обчислення площі S цієї криволінійної трапеції підставу AB (відрізок [a, b]) розбивають на n ділянок (необов'язково рівних) точками а = x 0 <x 1 <... <x n-1 <<x n = b, позначаючи довжини цих ділянок D x 1, D x 2, ..., D x n; на кожному такому ділянці будують прямокутники з висотами f (x1), f (x2), ..., f (x n) де x k - деяка точка з відрізка [xk - 1, xk] (на рис. заштрихован прямокутник, побудований на k-ій дільниці розбиття; f (xk) - його висота). Сума Sn площ побудованих прямокутників розглядається як наближення до площі S криволінійної трапеції:

S »Sn = f (x1) D x 1 + f (x2) D x 2 + f (x n) D xn

або, застосовуючи для скорочення запису символ суми S (грецька буква «сигма»):

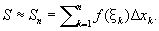
Зазначене вираз для площі криволінійної трапеції тим точніше, чим менше довжини D xk ділянок розбиття. Для знаходження точного значення площі S треба знайти межа сум Sn в припущенні, що число точок ділення необмежено збільшується і найбільша з довжин D xk прагне до нуля.

Відволікаючись від геометричного змісту розглянутої задачі, приходять до поняття визначеного інтеграла від функції f (x), безперервної на відрізку [а, b], як до межі інтегральних сум Sn при тому ж граничному переході. Цей інтеграл позначається

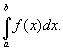
Символ ò (подовжене S - перша буква слова Summa) називається знаком інтеграла, f (x) - підінтегральною функцією, числа а і b називаються нижньою і верхньою межами певного інтеграла. Якщо а = b, то, за визначенням, вважають

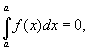
Крім того,

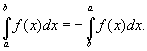
Властивості визначеного інтеграла:

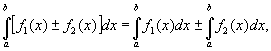
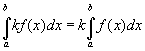
(K - постійна). Очевидно також, що

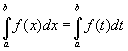
(Чисельне значення певного інтеграла не залежить від вибору позначення змінної інтегрування).

До обчислення певних інтегралів зводяться завдання про вимірі площ, обмежених кривими (завдання «знаходження квадратур»), довжин дуг кривих ( «випрямлення кривих»), площ поверхонь тіл, об'ємів тіл ( «знаходження кубатур»), а також завдання визначення координат центрів тяжіння , моментів інерції, шляхи тіла по відомій швидкості руху, роботи, виробленої силою, і багато інших завдань природознавства і техніки. Наприклад, довжина дуги плоскої кривої, заданої рівнянням у = f (x) на відрізку [a, b], виражається інтегралом

обсяг тіла, утвореного обертанням цієї дуги навколо осі Ox, - інтегралом

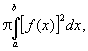
поверхню цього тіла - інтегралом

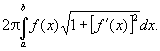
Фактичне обчислення певних інтегралів здійснюється різними способами. В окремих випадках певний інтеграл можна знайти, безпосередньо обчислюючи межу відповідної інтегральної суми. Однак здебільшого такий перехід до межі скрутний. Деякі певні інтеграли вдається обчислювати за допомогою попереднього відшукання невизначених інтегралів (див. Нижче). Як правило ж, доводиться удаватися до наближеного обчислення певних інтегралів, застосовуючи різні квадратурні формули (Наприклад, трапецій формулу , Сімпсона формулу ). Таке наближене обчислення може бути здійснено на ЕОМ з абсолютною похибкою, що не перевищує будь-якого заданого малого позитивного числа. У випадках, що не вимагають великої точності, для наближеного обчислення певних інтегралів застосовують графічні методи (див. графічні обчислення ).

Поняття визначеного інтеграла поширюється на випадок необмеженого проміжку інтегрування, а також на деякі класи необмежених функцій. Такі узагальнення називаються невласними інтегралами .

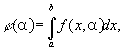
де функція f (x, a) неперервна по x називаються інтегралами, залежними від параметра. Вони служать основним засобом вивчення багатьох спеціальних функцій (Див., Наприклад, Гамма-функція ).

Невизначений інтеграл. Знаходження невизначених інтегралів, або інтегрування, є операція, зворотна диференціюванню. При диференціюванні даної функції шукається її похідна. При інтегруванні, навпаки, шукається первісна (або примітивна) функція - така функція, похідна якої дорівнює даній функції. Таким чином, функція F (x) є первісною для даної функції f (x), якщо F '(x) = f (x) або, що те ж саме, dF (x) = f (x) dx. Ця функція f (x) може мати різні первісні, але всі вони відрізняються один від одного тільки постійними складовими. Тому все Первісні для f (x) містяться в вираженні F (x) + С, яке називають невизначеним інтегралом від функції f (x) і записують

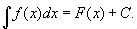
Певний інтеграл як функція верхньої межі інтегрування

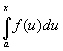
( «Інтеграл із змінною верхньою межею»), є одна з первісних підінтегральної функції. Це дозволяє встановити основну формулу І. і. (Формулу Ньютона - Лейбніца):

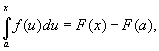
виражає чисельне значення певного інтеграла у вигляді різниці значень будь-якої первісної підінтегральної функції при верхній і нижній межах інтегрування.

Взаємно зворотний характер операцій інтегрування і диференціювання виражається рівністю

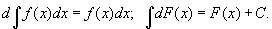
Звідси випливає можливість отримання з формул і правил диференціювання відповідних формул і правил інтеграції (див. Табл., Де C, m, a, k - постійні і m ¹ -1, а> 0).

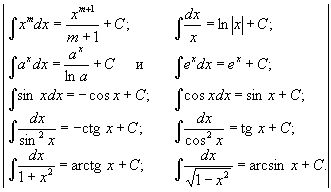
¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾

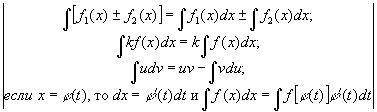
¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾

Труднощі І. і. в порівнянні з диференціальним численням полягає в тому, що інтеграли від елементарних функцій не завжди виражаються через елементарні, можуть не виражатися, як кажуть, «в кінцевому вигляді». І. і. має лише окремими прийомами інтегрування в кінцевому вигляді, область застосування кожного з яких обмежена (способи інтегрування викладаються в підручниках математичного аналізу: обширні таблиці інтегралів наводяться в багатьох довідниках).

До класу функцій, інтеграли від яких завжди виражаються в елементарних функціях, належить безліч всіх раціональних функцій

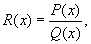
де P (x) і Q (x) - многочлени. Багато функцій, які не є раціональними, також інтегруються в кінцевому вигляді, наприклад функції, раціонально залежать від

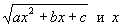
або ж від x і раціональних ступенів дробу

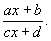
В кінцевому вигляді інтегруються і багато трансцендентні функції, наприклад раціональні функції синуса і косинуса. Функції, які зображаються невизначеними інтегралами, що не беруть в кінцевому вигляді, являють собою нові трансцендентні функції. Багато з них добре вивчені (див., Наприклад, інтегральний логарифм , Інтегральний синус і інтегральний косинус , Інтегральна показова функція ).

Поняття інтеграла поширюється на функції багатьох дійсних змінних (див. кратний інтеграл , криволінійний інтеграл , поверхневий інтеграл ), А також на функції комплексного змінного (див. аналітичні функції ) І вектор-функції (див. векторне числення ).

Про розширення і узагальнення поняття інтеграла див. Ст. інтеграл .

Історична довідка. Виникнення завдань І. і. пов'язане із знаходженням площ і обсягів. Ряд завдань такого роду було вирішено математиками Стародавньої Греції. Антична математика передбачила ідеї І. і. в значно більшому ступені, ніж диференціального обчислення. Велику роль при вирішенні таких завдань грав вичерпання метод , створений Евдоксом Кнідським і широко застосовувався Архімедом . Однак Архімед не надала загального змісту інтеграційних прийомів і поняття про інтеграл, а тим більше не створив алгоритму І. і. Вчені Середнього і Близького Сходу в 9-15 ст. вивчали і перекладали праці Архімеда на загальнодоступний в їх середовищі арабську мову, але істотно нових результатів в І. і. вони не отримали. Діяльність європейських вчених в цей час була ще більш скромною. Лише в 16 і 17 ст. розвиток природних наук поставило перед математикою Європи ряд нових завдань, зокрема завдання на знаходження квадратур, кубатури і визначення центрів ваги. Праці Архімеда, вперше видані в 1544 (латинською і грецькою мовами), стали залучати широке увагу, і їх вивчення стало одним з найважливіших відправних пунктів подальшого розвитку І. і. античний «Неподільних» метод був відроджений І. Кеплером . У більш загальній формі ідеї цього методу були розвинені Б. Кавальєрі , Е. Торрічеллі , Дж. Валлісом , Б. Паскалем . Методом «неподільних» було вирішено ряд геометричних і механічних завдань. До цього ж часу відносяться опубліковані пізніше роботи П. ферма по квадрірованію парабол n-го ступеня, а потім - роботи Х. Гюйгенса по випрямлення кривих.

В результаті цих досліджень виявилася спільність прийомів інтегрування при вирішенні зовні несхожих завдань геометрії і механіки, що приводилися до квадратури як до геометричного еквіваленту певного інтеграла. Заключним ланкою в ланцюзі відкриттів цього періоду було встановлення взаємно зворотного зв'язку між завданнями на проведення дотичної і на квадратуру, т. Е. Між диференціюванням і інтеграцією. Основні поняття і алгоритм І. і. були створені незалежно один від одного І. Ньютоном і Г. Лейбніцем . Останньому належить термін «інтегральне числення» і позначення інтеграла ò ydx.

При цьому в роботах Ньютона основну роль грало поняття невизначеного інтеграла (флюенти, см. флюксій числення ), Тоді як Лейбніц виходив з поняття певного інтеграла. Подальший розвиток І. і. в 18 ст. пов'язане з іменами І. Бернуллі і особливо Л. Ейлера . На початку 19 ст. І. і. разом з диференціальним численням було перебудовано О. Коші на основі теорії меж. У розвитку І. і. в 19 ​​ст. взяли участь російські математики М. В. Остроградський , В. Я. Буняковский , П. Л. Чебишев . В кінці 19 - початку 20 ст. розвиток теорії множин і теорії функцій дійсного змінного привело до поглиблення і узагальнення основних понять І. і. (Б. Ріман , А. Лебег та ін.).

Літ .: Історія. Ван дер Варден Б. Л., пробуджує наука, пров. з голл., М., 1959; Вілейтнер Г., Історія математики від Декарта до середини 19 століття, пров. з нім., 2 вид., М., 1966; Будівництв Д. Я., Короткий нарис історії математики, пер. з нім., 2 вид., М., 1969; Cantor М .. Vorleslingen ü ber Geschichte der Mathematik, 2 Aufl., Bd 3-4, Lpz. - B., 1901-24.

Роботи основоположників і класиків І. і. Ньютон І., Математичні роботи, пер. з латин., М.-Л., 1937; Лейбніц Г., Вибрані уривки з математичних творів, пров. с. латин., «Успіхи математичних наук», 1948, т. 3, ст. 1; Ейлер Л., Інтегральне числення, пер. з латин., тт. 1-3, М., 1956-58; Коші О. Л., Короткий виклад уроків про диференціальному і інтегральному численні, пров. з франц., СПБ, 1831; його ж, Алгебраїчний аналіз, пров. з франц., Лейпциг, 1864.

Підручники та навчальні посібники з І. і. Хинчин Д. Я., Короткий курс математичного аналізу, 3 вид., 1957; Смирнов В. І., Курс вищої математики, 22 вид., Т. 1, М., 1967; Фихтенгольц Г. М., Курс диференціального й інтегрального числення, 7 видавництво., Т. 2, М., 1969; Ільїн В., Позняк Е. Р., Основи математичного аналізу, 3 вид., Ч. 1, М., 1971; Курант Р., Курс диференціального й інтегрального числення, пров. з нім. і англ., 4 видавництва., т. 1, М., 1967; Двайт Г.-Б., Таблиці інтегралів і інші математичні формули, пров. з англ., М., 1964.

За редакцією академіка А. Н. Колмогорова.

Мал. до ст. Інтегральне числення.